Introduction

In a previous article, we discussed symmetric encryption. In this article we’ll take a look at asymmetric encryption and in particular public key encryption.

In symmetric encryption, the same secret key is used for both encoding and decoding messages. However, as we discussed in the previous article, transmitting this secret key securely can be challenging. One solution to this problem is asymmetric encryption, which involves the use of two keys: a public key, which is openly accessible, and a private key, which is kept secret.

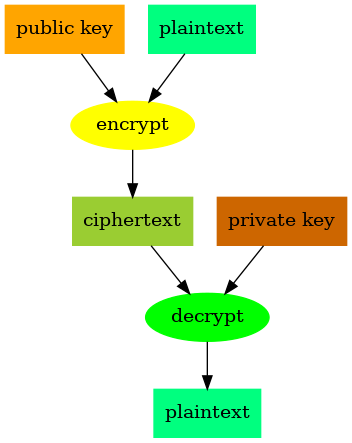
The two keys are mathematically linked, plaintext encrypted with a user’s the public key can only be decrypted with their corresponding private key. Likewise, plaintext encrypted with the user’s private key can only be decrypted with the corresponding public key.

The former is used in a public key encryption system, and will be the subject of this article. The latter is used in a digital signature system which will be discussed in the next article.

Public Key Encryption

In a public key encryption system, participants distribute their public keys freely but keep their private keys secret. Anyone who wants to send a message to a recipient will encrypt it using their public key. Only the private key can be used to decrypt the resulting ciphertext and as long as the recipient keeps their private key secret, only they can decrypt the message.

[source]

There are different types of algorithms that are used to implement public key encryption. In general, their security relies on the mathematical properties that can be used to design puzzles that are too computationally demanding to solve as they lack a known efficient solution.

For example, one of the pioneering techniques known as RSA relies on the fact that it is extremely difficult to factorize large integer numbers.

Because public key encryption is computationally intensive, in situations where lengthy messages or frequently exchanged messages need to be encrypted, public key encryption is used to initially send a secret key to the recipient. Subsequent communication can then more efficiently use the shared secret key for symmetric encryption.

Uses

Some uses of public key encryption:

• A prominent use of public key encryption is the issuing and validation of certificates used to establish secure web communication via SSL/TLS

• Encrypted email technologies such as PGP rely on public key encryption.

• In blockchain systems, accounts are represented by a public/private key pair. The public key is transformed into the account’s address while the private key is used by the account owner to verify transactions.

Examples in code

Here we look at examples in Python and JavaScript.

Python

from cryptography.hazmat.primitives.asymmetric import rsa, padding
from cryptography.hazmat.primitives import hashes

private_key = rsa.generate_private_key(public_exponent=65537, key_size=2048)
public_key = private_key.public_key()

plaintext_in = "The quick brown fox jumps over the lazy dog"


def encrypt(plaintext, public_key):
    return public_key.encrypt(
        plaintext,
        padding.OAEP(
            mgf=padding.MGF1(algorithm=hashes.SHA256()),
            algorithm=hashes.SHA256(),
            label=None,
        ),
    )


ciphertext = encrypt(bytes(plaintext_in, "utf-8"), public_key)


def decrypt(ciphertext, private_key):
    return private_key.decrypt(
        ciphertext,
        padding.OAEP(
            mgf=padding.MGF1(algorithm=hashes.SHA256()),
            algorithm=hashes.SHA256(),
            label=None,
        ),
    )


bytes_out = decrypt(ciphertext, private_key)
plaintext_out = bytes_out.decode("utf-8")

assert plaintext_in == plaintext_out  # should be equal

[source file]

In python, we use the third party library cryptography that can be installed via:

pip install cryptography

The first step is generating a recipient’s public/private key pair using the RSA algorithm. We then encrypt the plaintext using the public key and finally decrypt the ciphertext using the private key.

Additional parameters required for the RSA such as public exponent, key size and padding are also chosen to be common ones. One has to be careful setting these and a detailed understanding of the underlying algorithms is required.

const { 
    generateKeyPairSync,
    publicEncrypt,
    privateDecrypt,
    constants
} = await import("node:crypto");

const { publicKey, privateKey } = generateKeyPairSync('rsa', {
    publicExponent: 65537,
    modulusLength: 2048,
});

let plaintextIn = "The quick brown fox jumps over the lazy dog";

const encrypt = (plaintextBytes, publicKey) => {
    return publicEncrypt({
	key: publicKey,
	padding: constants.RSA_PKCS1_OAEP_PADDING,
	oaepHash: 'sha256',
    }, plaintextBytes);
};

let ciphertext = encrypt(Buffer.from(plaintextIn), publicKey);

const decrypt = (ciphertext, privateKey) => {
    return privateDecrypt({
	key: privateKey,
	padding: constants.RSA_PKCS1_OAEP_PADDING,
	oaepHash: 'sha256',
    }, ciphertext);
};

let bytesOut = decrypt(ciphertext, privateKey);
let plaintextOut = bytesOut.toString();

console.assert(plaintextIn == plaintextOut); // should pass

[source file]

In JavaScript, we use the crypto module that by default ships with NodeJS.

Similar to the Python example, we first generate a key pair, then encrypt with the public key and decrypt with the private key.

Conclusion

This article discusses the basics of asymmetric encryption and in particular public key encryption. Code samples are provided in Python and JavaScript demonstrating public key encryption. For a more in-depth exploration, checkout the CRYPTO101 course and the Cryptopals challenge.